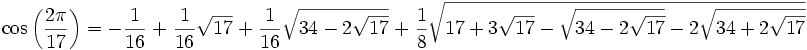Biographies of Gauss
- Wikipedia
article
"Gauss was a child prodigy. There are many
anecdotes pertaining to his precocity while a toddler, and he
made his first ground-breaking mathematical discoveries while
still a teenager. He completed Disquisitiones Arithmeticae,
his magnum opus, in 1798 at the age of 21, though it would not
be published until 1801. This work was fundamental in
consolidating number theory as a discipline and has shaped the
field to the present day."
- MathWorld
article
"German mathematician who is
sometimes called the 'prince of mathematics.' He was a
prodigious child, at the age of three informing his father of
an arithmetical error in a complicated payroll calculation and
stating the correct answer. In school, when his teacher gave
the problem of summing the integers from 1 to 100 (an
arithmetic series) to his students to keep them busy, Gauss
immediately wrote down the correct answer 5050 on his
slate. At age 19, Gauss demonstrated a method for constructing
a heptadecagon using only a straightedge and compass which had
eluded the Greeks."
- St. Andrews
biography
"At the age of seven, Carl Friedrich Gauss
started elementary school, and his potential was noticed
almost immediately. His teacher, Büttner, and his assistant,
Martin Bartels, were amazed when Gauss summed the integers
from 1 to 100 instantly by spotting that the sum was 50 pairs
of numbers each pair summing to 101."
- Geocities
biography Includes a list
of formulas discovered by Gauss
"From the outside, Gauss' life was
very simple. Having brought up in an austere childhood in a
poor and uneducated family he showed extraordinary
precocity. He received a stipend from the duke of Brunswick
starting at the age of 14 which allowed him to devote his time
to his studies for 16 years. Before his 25th birthday, he was
already famous for his work in mathematics and astronomy. When
he became 30 he went to Göttingen to become director of the
observatory. He rarely left the city except on scientific
business. From there, he worked for 47 years until his death
at almost 78. In contrast to his external simplicity, Gauss'
personal life was tragic and complicated. Due to the French
Revolution, Napoleonic period and the democratic revolutions
in Germany, he suffered from political turmoil and financial
insecurity. He found no fellow mathematical collaborators and
worked alone for most of his life. An unsympathetic father,
the early death of his first wife, the poor health of his
second wife, and terrible relations with his sons denied him a
family sanctuary until late in life."
"Even with all of these troubles, Gauss kept an amazingly rich
scientific activity. An early passion for numbers and
calculations extended first to the theory of numbers, to
algebra, analysis, geometry, probability, and the theory of
errors. At the same time, he carried on intensive empirical
and theoretical research in many branches of science,
including observational astronomy, celestial mechanics,
surveying, geodesy, capillarity, geomagnetism,
electromagnetism, mechanism optics, actuarial science. His
publications, abundant correspondence, notes, and manuscripts
show him to have been one of the greatest scientific virtuosos
of all time."
- Carl
Friedrich Gauss: Titan of Science by G. Waldo Dunnington, Jeremy
Gray and Fritz-Egbert Dohse
- Gauss:
A Biographical Study by W. K. Bühler
The law of quadratic recipocity, Gauss' "Golden Theorem"
- Wikipedia
article "The law of quadratic reciprocity is a theorem from
modular arithmetic, a branch of number theory, which gives
conditions for the solvability of quadratic equations modulo
prime numbers."
- "Proofs
of quadratic reciprocity In the mathematical field of number
theory, the law of quadratic reciprocity, like the Pythagorean
theorem, has lent itself to an unusual number of proofs. Several
hundred proofs of the law of quadratic reciprocity have been
found."
- MathWorld
article "Also called the aureum theorema (golden theorem) by
Gauss."
-
Gauß, Eisenstein, and the ``third'' proof of the Quadratic Reciprocity
Theorem: Ein kleines Schauspiel
A short play written by my
friend and former student David J. Pengelley and Reinhard
C. Laubenbacher in 1994.
- A brief summary from the book
NUMBER THEORY WITH COMPUTER APPLICATIONS by Ramanujachary Kumanduri and Cristina Romero
"The elementary properties of quadratic congruences and a method
for their solution were studied in a previous chapter. Now, we focus our
attention on some deeper properties of numbers that were discovered by Euler,
Legendre, and Gauss. The simplest of these are the following.
- The odd prime divisors of numbers of the form
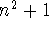 are of the
form 4k+1.
are of the
form 4k+1. - The odd prime divisors of numbers of the form
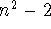 are of the form
8k+1 or 8k-1. are of the form
8k+1 or 8k-1. - The odd prime divisors (also not 3) of
numbers of the form
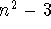 are of the form 12k+1 or 12k-1.
are of the form 12k+1 or 12k-1. - The prime divisors (not
equal to 2 or 5) of numbers of the form
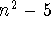 are of the form 20k+1, 20k-1,
20k+9 or 20k-9. are of the form 20k+1, 20k-1,
20k+9 or 20k-9.
Generalizing these results, Euler conjectured that the prime divisors p
of
numbers of the form 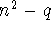 are of the form are of the form 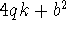 or or 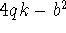 , for some
odd b. This is the Quadratic Reciprocity Law. The first complete proof
of
this law was given by Gauss in 1796. Gauss gave eight different proofs of the
law and we discuss a proof that Gauss gave in 1808." , for some
odd b. This is the Quadratic Reciprocity Law. The first complete proof
of
this law was given by Gauss in 1796. Gauss gave eight different proofs of the
law and we discuss a proof that Gauss gave in 1808."
|
The heptadecagon (17-sided polygon), Gauss' first mathematical triumph
- Compass and
straightedge - the regular Heptadecagon YouTube video (1:39)
showing the ruler and compass construction set to music.
Unfortunately, the aspect ratio is wrong, making the circles look
like ellipses. The YouTube site has
a written explanation of the
construction, which is not easy to follow otherwise.
- All the
possible polygons! YouTube video (4:48) showing ruler and
compass constructions of all possible n-gons
for n ≤ 51.
- Wikipedia
article on Ruler and compass constructions Includes Gauss'
formula
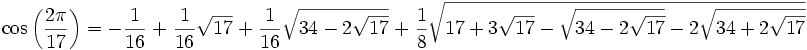
- Construction
of the 17-gon
"Although mathematicians have been working on
this problem in Euclid's time (300 B.C.E.), it was Gauss who
discovered it's construction in 1796 when he was an
eighteen-year-old. Another significance is it is by this discovery
that Gauss decided to spend him life persuing mathematics."
- More
detailed Wikipedia article
"Carl Friedrich Gauss
proved - as a 19 year old student at Göttingen University -
that the regular heptadecagon (a 17 sided polygon) is
constructible with a pair of compasses and a straightedge."
- Another
Wikipedia article with graphic animations of the
construction and that of the pentagon.
- MathWorld
article
"Gauss's proof appears in his monumental work
Disquisitiones Arithmeticae. The proof relies on the property of
irreducible polynomial equations that roots composed of a finite
number of square root extractions only exist when the order of the
equation is a product of the form... "
|
Finding the orbit of the
asteroid Ceres, discovered on the night of January 1, 1801.
This
made Gauss a celebrity in Europe.
- How
Gauss Determined the Orbit of CeresVeronique Le Corvec, Jeffrey
Donatelli and Jeffrey Hunt, 15 page slide presntation.
- The
Discovery of Ceres: How Gauss Became Famous by Donald Teets and
Karen Whitehead. 11 page article from Mathematics Magazine,
Vol. 72, No. 2 (Apr., 1999): pp. 83-93.
- The
Discovery of Ceres Short online article with moving illustrations
of the geometry involved from Kepler's Discovery .
"Gauss discovered a method for computing the planet's orbit
using only three of the original observations and successfully
predicted where Ceres might be found."
"The prediction catapulted
him to worldwide acclaim, due, in the words of biographer
W. K. Bühler, 'to the popular appeal which astronomy has always
enjoyed,' and launched one of the most fruitful careers in the history
of science."
- Gauss
and Ceres by Leorah Weiss. A short account written by a student
at Rutgers.
"... for it is now clearly shown that the orbit of a
heavenly body may be determined quite nearly from good observations
embracing only a few days; and this without any hypothetical
assumption."
- Carl Friedrich Gauss
- Gauss's
Orbits Short article by Ivars Peterson
"With a major
mathematical work just published and little else to occupy his time
during the latter part of 1801, Gauss brought his formidable powers
to bear on celestial mechanics. Like a skillful mechanic, he
systematically disassembled the creaky, ponderous engine that had
long been used for determining approximate orbits and rebuilt it into
an efficient, streamlined machine that could function reliably given
even minimal data."
|
Disquisitiones Arithmeticae, 1801, the most
important book in mathematics since Newton's Principia.
Gauss
finished writing it when he was 21.
|
Gauss and the prime number
theorem
- How Many Primes Are
There? A short introduction to the problem
"Gauss was also studying prime tables and came up with a different
estimate (perhaps first considered in 1791), communicated in a
letter to Encke in 1849 and first published in 1863.
- Gauss:
- pi(x) is approximately Li(x) (the
principal value of integral of 1/log u from u=0 to
u=x)."
- MathWord
article
"In 1792, when only 15 years old, Gauss proposed that
..."
- Wikipedia
article
"Carl Friedrich Gauss considered the same question and,
based on the computational evidence available to him and on some
heuristic reasoning, he came up with his own approximating function,
the logarithmic integral li(x), although he did not publish his
results."
|
|